Shimano, Campagnolo, and SRAM offer 11 speed road groups with the following chainrings combos: 53/39, 52/36, and 50/34. Which is great, but then the question arises:
How bad will it be if I mount a 53/36 combo?
The following analysys has Shimano in mind, but the result is likely nearly the same for any brand. It tries to derive some tangible estimate of the "penalty" for combining chainrings with greater differences than the standard combinations.
The assumption here is that the front derailleur can handle almost any combination of chainrings with very little difficulty. That is, the front derailleur is not the limiting factor of why they don't offer certain combinations with larger tooth difference.
The limit is imposed by the geometry of the chain-line and chainrings: At some point, when you are in the small chainring and want to use the smallest cassette cog, the chain starts rubbing against the big ring.

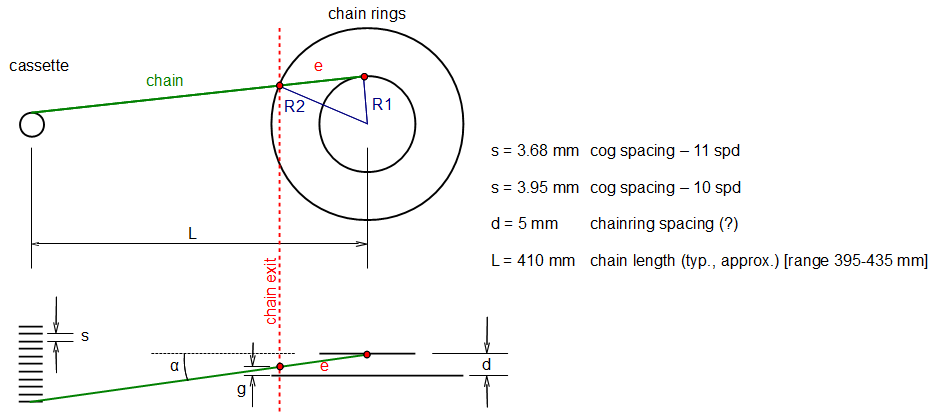
The length of chain $e$ that has left the small ring, but has not "exited" the perifery of the big ring is: $$e(n_2, n_1) = \sqrt{R_2^2 - R_1^2} = q.\sqrt{n_2^2-n_1^2}$$ where $q = \hbox{12.7 mm} / 2\pi = \hbox{2.02 mm}$ and $n$ is the number of teeth on the big and small chainrings, respectively. Now, if the cogs on the cassette are spaced by $s$ and the spindle to rear axle distance is $L$, then one gear shift results in this much movement of the chain near the exit point $E$: $$u(n_2, n_1) = e {s \over L} = {s.q \over L} \sqrt{n_2^2 - n_1^2}$$ In other words this is how much one gear shift at the back "costs", in terms of bringing the chain closer or farther from rubbing against the big chainring. So how much then does a change in the value of $e$ cost? Well, for a perfectly symmetrically alligned 11-speed drive train, while in the smallest cog the chain angle is: $$\alpha = {(5s + d/2) \over L}$$ This is for halph big ring spacing plus five cog shifts. Thus the gap (or lack thereof) between the chain and the big ring at the exit point depends on the $e$ like this: $$g(n_2, n_1) \sim -\alpha .e = -{(5s+d/2). q \over L}\sqrt{n_2^2-n_1^2}$$ Note that the above formula does not claim to compute $g$ - it is missing some additive constant. But, what we really care for is how much $g$ changes as we switch between chainring combinations. For example, we might care for $g(53,39)-g(53,36)$ - how much will the gap decrease, if I swap in a smaller inner chainring. But even this is not very useful, because it will give us some distance in mm - so what?! We need a better, more easily interpretable unit, against which to measure the gap. This unit is $u$ from above - "the gap change per one gear shift". In other words, the "relative penalty" of using a smaller inner chainring compared against shifting by one cog at the back is: $$ p = {g(n'_2, n'_1) - g(n''_2, n''_1) \over u(n_2, n_1)} = (5 + {d \over 2s}) {\sqrt{{n''_2}^2-{n''_1}^2}-\sqrt{{n'_2}^2-{n'_1}^2} \over \sqrt{n_2^2-n_1^2}} $$ where in the denominator one can choose either of the $(n_2, n_1)$ pairs, depending on what one wants to ask, but in reality the $u$ values vary relatively little, so the result almost doesn't change, whichever pair is chosen.
Notice that in the end many constants just cancelled out! And luckily, those were exactly the ones that were most approximate and potentially subject to objections regarding their exact values. In fact, all that is left is the ratio $d/2s$. And for the 10-speed case, we would not have even that.
from math import *
s = 3.68
q = 12.7/(2*pi)
d = 5.0
def gete(n2, n1):
return q * sqrt(abs(n2*n2-n1*n1))
def getu(n2, n1, L = 410.0):
return (s*q/L)*sqrt(abs(n2*n2-n1*n1))
def getDeltaG11(n2a, n1a, n2b, n1b, cog = 5.0, L = 410.0):
# Gap change between two chainring sets; cog = [-5...+5]
return (cog*s + d/2.) * q / L * ( sqrt(abs(n2a*n2a - n1a*n1a)) - sqrt(abs(n2b*n2b - n1b*n1b)) )
# Then p(53,39, 52,36) = getDeltaG11(53,39, 52,36)/getu(53,39)
Now, let us get a feeling of the actual lengths and distances in mm. Start with $e$, the chain section that is behind the big chainring:
>>> gete(53,39) ... 72.540707016919797 mm >>> gete(52,36) ... 75.844689898533943 mm >>> gete(50,34) ... 74.100900712811935 mm >>> gete(53,36) ... 78.621860482207367 mmSame for the $u$-s, the amount by which the chain moves closer or farther from the big chainring as a result of a single gear shift by the rear derailleur:
>>> getu(53,39), getu(52,36), getu(50,34), getu(53,36), "all in mm" (0.65109707761528013, 0.68075233860147544, 0.66510076737353163, 0.70567913798664184, 'all in mm')Let's see the $\Delta g$-s - how much the chain gap decreases for the small-small combination, for various chainring combos, compared to a 53/39:
>>> getDeltaG11(53,39, 52,36) ... -0.1684225420139894 mm >>> getDeltaG11(53,39, 50,34) ... -0.079531824985721519 mm >>> getDeltaG11(53,39, 53,36) ... -0.30999050591344024 mmThis is, strictly speaking, the answer to our original question, but what do those gap changes mean in practice? The numbers that we really care for are the "penalties", the $p$-s, i.e. the gap chanegs as a fraction of a single gear shift at the back:
>>> getDeltaG11(53,39, 52,36)/getu(53,39) ... -0.25867500838869811 >>> getDeltaG11(53,39, 50,34)/getu(53,39) ... -0.12215048680147085 >>> getDeltaG11(53,39, 53,36)/getu(53,39) ... -0.47610489521595928Or, in plain words, compared to a 53/39 chainring, switching to a:
"One looses 1/4, 1/8, and 1/2 gears from the cassette"
Note that in many configurations there may not have been any "gap" to begin with! This calculation just tells us how much worse things get. If there was chain rubbnig before, then it will be that much more after.
A similar computation can be made for any other cog, i.e. next-to-smallest, two cogs from the smallest, etc. It should be obvious that $p$ will only decrease, as we will be replacing the leading term $(5+d/2s)$ with $(m+d/2s)$, where $m = 5, 4, 3, ... $ For example, for the next to last cog, the penalties decrease to 1/5, 1/10, and 2/5, respectively.
I find this article rather interesting, plus they have a nice picture of the chain and rings: Tech Breakdown: How 135mm Rear Hub Spacing Affects Road Bike Chainline & Shifting
This is directly related to the above : About Bicycle Chainline. This is also how I came up with the 5 mm chainring spacing.